QS 026 Permutation & Combination : Combinations

A general concept about combination is counting a number of possibility without replacing and most importantly, the arrangements don't matter.

Let's watch this useful video, may it helps you perceive combination better...

QS026 Permutation & Combination : Factorial

This is another basic principle a student must possess before going deeper into the Permutations and Combination chapter. View this video for further explanation.

After understanding this fundamental, we will learn better about Permutation & Combination

QS026 Numerical Method - Newton Raphson Method

This method is used to approximate a certain root of an equation. This is done by find it's derivative and putting it in
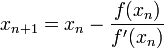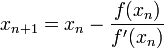Technically this is a tedious method with repetition of numerical computation. Students tends to make mistake. However with the usage of "Calculate" option in today's scientific calculator, mistakes can be minimize.

Basically we need to approximate the initial value and hope that the value will be reduced to the root instead of converging.

Please see this useful video on Newton-Raphson Method...

QS026 Numerical Method - Trapezium Rule

In this first sub-topic of Chapter 7, basically matriculation students are exposed to an alternative numerical method to find the area under a certain graph. Normally we would use integration as the fastest and more accurate way of finding area under the graph.

Trapezium rule however, introduce an alternative where we actually break the area under the graph into several trapezium. Instead of integrating, we add all those trapezium areas together to sums up the equivalent area under the graph.

Remember the value gained does not necessarily be the same as trapezium rule actually gets the approximate area under the graph only. Interesting method nonetheless and the easier way for some functions that has difficult integrations.

This video will give you better step-by-step explanation.

QS026 Differential Equations - Integrating Factor

If a First Order Linear Equation can't be separated, then comes the Differential using the Integrating Factor:

• Identify the integrating factor.
• Multiply both sides of the equation with the integrating factor, then;
• Integrate both sides of the equation.

Observe the video for better explanation.

There you have it, two noticable techniques in Differential Equation in Chapter 6 of QS026 Matriculation Mathematics.

QS026 Differential Equations - Separable Variable

Basic Concept of Separable Variable is:

• The equations should be able to be separated to two different sides then,
• Integrate...

It's that simple...

follow this simple explanation...

See? Very easy...

Good Luck